Python Optimisation Patterns
Array Broadcasting (Vectorisation)
The manner by which NumPy stores data in arrays enables its functions to utilise array broadcasting (more broadly known as vectorisation), whereby the processor executes one instruction across multiple variables simultaneously, for every mathematical operation between arrays. Array broadcasting can perform mathematical operations many times faster, however it requires using supported functions.
Read MoreList Comprehension
List comprehension (e.g. [expression for item in iterable if condition == True]) is faster than constructing a list with a loop. It can’t be used for all list constructions, such as where items depend on one another, but it should be used whenever possible.
Searching with a for-loop
Searching for an element in a sequence (e.g. a list) with a for-loop and an equality check is very natural, but Python has a built-in in keyword which should be used whenever possible.
Set
Similar to the mathematical concept of a set, Python (and most other languages) provides a data structure set which is an unordered collection of unique values. Using a set is the fastest way to detect unique items (e.g. if a in my_set) or remove duplicates (e.g. [x for x in set(my_list)]).
Use numpy.array, rather than Python list, with NumPy functions
NumPy functions are designed to work with NumPy classes (e.g. numpy.array), whilst many work with core Python classes (e.g. list) this normally incurs an additional cost of NumPy first converting the argument to the corresponding NumPy type.
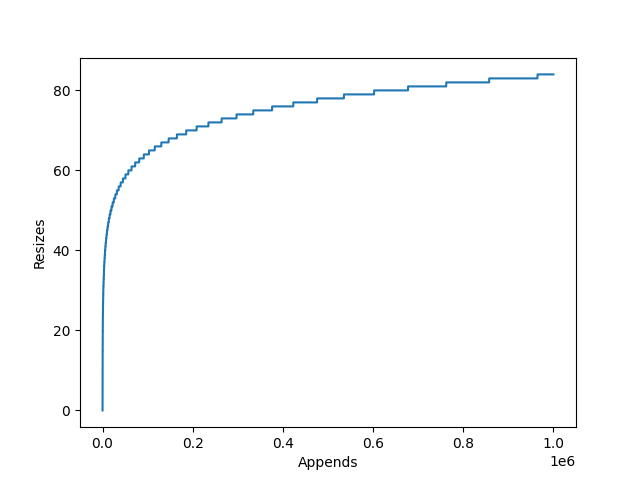
numpy.array.resize()
NumPy’s arrays are static arrays which, unlike core Python’s lists, do not dynamically resize.
If you wish to append to a NumPy array, you must call resize() first, which can lead to performance issues.
If a user treats array.resize like list.append, resizing for each individual append, they will be performing significantly more copies and memory allocations and hence make your code slower.
Tuple
In addition to lists, Python has the concept of tuples. These are immutable static arrays, they cannot be resized, nor can their elements be changed. Their potential use-cases are greatly reduced due to these two limitations, as they are only suitable for groups of immutable properties.
Tuples will typically allocate several times faster than lists with equal contents, therefore they are an ideal replacement if immutable lists are being created thousands of times (tuples are unlikely to make a huge difference to any individual list allocation).
Read MoreUse Numba to precompile and optimise Python functions
Numba is an open-source Just In Time (JIT) compiler which converts Python functions into optimised machine code at runtime. At its simplest, it can be invoked by simply adding the @njit decorator from the numba package before your function declarations.