False Sharing

Due to how caching works in modern processors, multiple threads accessing values stored consecutively in memory can result in false sharing where threads do not have truly parallel access which impacts performance. To avoid this, it is recommended that data parallel workloads are subdivided, such that consecutive elements are assigned to the same thread. This would typically be achieved via selecting a larger chunk size, or switching the order of a nested loop.

Other approaches may involve padding structures, by adding redundant variables, to ensure that variables fall into different cache lines. Several compilers also provide methods to hint how memory should be aligned.

Example Code

In the below example the outer loop on the variable i has been parellelised over the outer loop, when filling a 1000x1000 matrix. It is structured such that the inner loop does not access consecutive values. Therefore by parallelising the outer loop, it is likely that false sharing will occur as threads with consecutive values of i will access consecutive variables in memory.

const int N = 1000; // Matrix size

// Allocate a 2D matrix as a flattened 1D array
double *matrix = (double*)malloc(N * N * sizeof(double));

// Parallel loop with potential for false sharing
#pragma omp parallel for
for (int i = 0; i < N; ++i) {
    for (int j = 0; j < N; ++j) {
        matrix[j * N + i] = i + j;
    }
}

By changing the order in which matrix is accessed by i and j, such that each inner loop iterates consecutive variables, the potential for false sharing in this scenario can be greatly reduced.

        matrix[i * N + j] = i + j;

In this scenario reducing the potential for false sharing produced a 4x speedup when tested.

Example Benchmark

The below code provides expands the above example into a simple benchmark.

#include <cstdlib>
#include <iostream>
#include <omp.h>
#include <ostream>

int main() {
    const int N = 1000; // Matrix size
    const int num_threads = 8;

    // Allocate a 2D matrix as a flattened 1D array
    double *matrix = (double*)malloc(N * N * sizeof(double));

    // Warmup, this ensures OpenMP is initialised before timing execution
#pragma omp parallel for num_threads(num_threads)
    for (int i = 0; i < N * N; ++i) {
        matrix[i] = 0;
    }

    // Benchmarking
    const int iterations = 10;
    double total_time_without = 0.0, total_time_with = 0.0;

    for (int iter = 0; iter < iterations; ++iter) {
        double start_time = omp_get_wtime();
        // Parallel loop with potential for false sharing
#pragma omp parallel for num_threads(num_threads)
        for (int i = 0; i < N; ++i) {
            for (int j = 0; j < N; ++j) {
                matrix[j * N + i] = i + j;
            }
        }
        double mid_time = omp_get_wtime();
        // Parallel loop without potential for false sharing
#pragma omp parallel for num_threads(num_threads)
        for (int i = 0; i < N; ++i) {
            for (int j = 0; j < N; ++j) {
                matrix[i * N + j] = i + j;
            }
        }
        double end_time = omp_get_wtime();

        // Process timing
        total_time_with += (mid_time - start_time);
        total_time_without += (end_time - mid_time);
    }

    // Print the elapsed time
    std::cout << "Elapsed time with: " << total_time_with << " seconds" << std::endl;
    std::cout << "Elapsed time without: " << total_time_without << " seconds ";
    std::cout << "(" << total_time_with/total_time_without << "x faster)" << std::endl;

    return EXIT_SUCCESS;
}

#ifndef _OPENMP
#error This benchmark requires OpenMP support, ensure it is enabled inside compile settings 
#endif

In testing this produced the following results

Elapsed time with: 0.0131083 seconds
Elapsed time without: 0.0030481 seconds (4.30048x faster)

Reordering accesses of matrix to avoid false sharing executed over 4x faster.

The Technical Detail

Modern processors do not directly access variables inside a computers RAM, instead variables are loaded through layers of caches. These caches, L1, L2 & L3 increase in size and get slower with their number. Each CPU core (which can be considered a proxy for a thread), Some of these caches (e.g. L1) are per-core, whereas others (e.g. L3) are shared by all cores CPU.

Figure 1: An abstract visualisation of how memory reaches a thread for computation from RAM within a CPU.

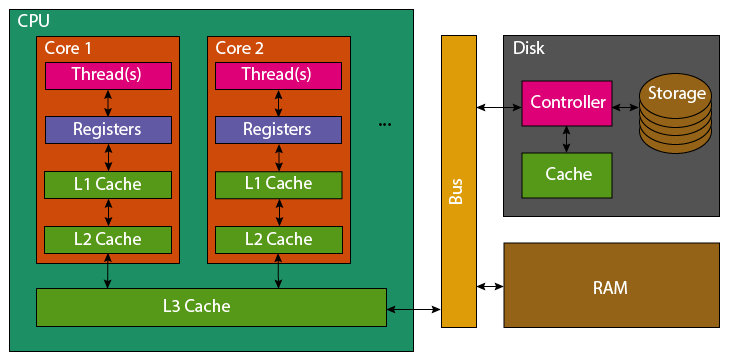
When a variable is accessed, a full 64 byte cache-line is loaded from the RAM (a typical variable is 4 or 8 bytes). This is stored first in the shared L3 cache, then L2 and subsequently L1 for the relevant CPU core (computation is performed directly in the registers). If a second CPU core, accesses a variable in this same 64 byte cache-line, it will have to load the same cache line either from RAM or the shared L3 cache in to it’s own L1 cache and registers.

As each CPU core using that cache line holds a unique copy in their L1, if one core modifies a variable the cache line is invalidated in all the other cores. This forces them to reload the entire cache line before they can use it again.

If a 64 byte cache line contains 4-byte integers, it could be false shared by as many as 16 CPU cores simultaneously, causing the cache line be reloaded from memory 15 additional times. If instead, each core were assigned data from a unique cache-line, these redundant reloads would be avoided.